• Linear programming was developed by George B Dantzing (1947) during second world war.
• It has been widely used to find the optimum resource allocation and enterprise combination.
• The word linear is used to describe the relationship among two or more variables which are directly proportional. For example, doubling (or tripling) the production of a product will exactly double (or triple) the profit and the required resources, then it is linear relationship.
• Programming implies planning of activities in a manner that achieves some optimal result with restricted resources.

Definition of L.P.

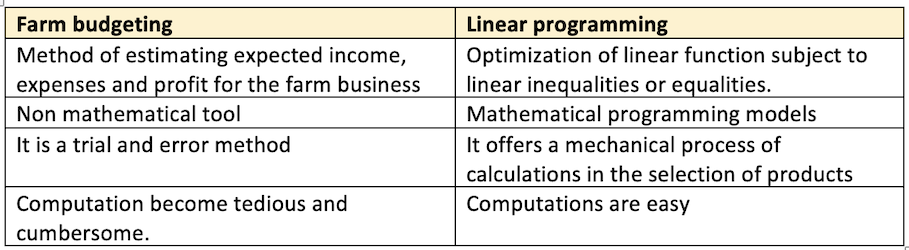
• Linear programming is defined as the optimization (Minimization or maximization) of a linear function subject to specific linear inequalities or equalities.
• LP is used in optimization problems like,
  • Minimization of Cost
  • Minimization of use of resources
  • Maximization of Profit

Assumptions of Linear Programming

• Linearity: It describes the relationship among two or more variables which are directly proportional.
• Additivity: Total input required is the sum of the resources used by each activity. Total product is sum of the production from each activity.
• Divisibility: Resources can be used in fractional amounts. Similarly, the output can be produced in fractions.
• Non negativity: Resources and activities cannot take negative values. That means the level of activities or resources cannot be less than zero.
• Finiteness of activities and resource restrictions: There is limit to the number of activities and resource constraints.
• Single value expectations: Resource supplies, input-output coefficients and prices are known with certainty.

Advantages of L.P.

• Allocation problems are solved.
• Provides possible and practical solution.
• Improves the quality of decisions.
• Highlights the constraints in the production.
• Helps in optimum use of resources.
• Provides information on marginal value products (shadow prices).

Limitations

• Linearity
• Considers only one objective for optimization.
• Does not consider the effect of time and uncertainty
• No guarantee of integer solutions
• Single valued expectations.

• Linear programming was developed by George B Dantzing (1947) during second world war.
• It has been widely used to find the optimum resource allocation and enterprise combination.
• The word linear is used to describe the relationship among two or more variables which are directly proportional. For example, doubling (or tripling) the production of a product will exactly double (or triple) the profit and the required resources, then it is linear relationship.
• Programming implies planning of activities in a manner that achieves some optimal result with restricted resources.

Definition of L.P.

• Linear programming is defined as the optimization (Minimization or maximization) of a linear function subject to specific linear inequalities or equalities.
• LP is used in optimization problems like, …

Yo! You just found a 20% discount using 👉 EASTEREGG

High-quality fitted cotton shirt produced by Next Level Apparel