• It is the systematic way of showing the relationship between different amounts of inputs that can be used to produce a product and the corresponding output of that product.
• Definition: Production function is a technical and mathematical relationship describing the manner and the extent to which a particular product depends upon the quantities of inputs or input services, used at a given level of technology and in a given period of time. In short, the relationship between input and output is termed as production function.

Types of Production Functions

Continuous Production Function:

• This is obtained for those inputs which can be split up in to smaller units.
• All those inputs which are measurable give raise to continuous production function.
• Example: Fertilizers, Seeds, Plant protection chemicals, Manures, Feeds etc.

Discontinuous or discrete Production Function

• Such a function is obtained for resources or work units which are used or done in whole numbers. In other words, production function is discrete, where inputs cannot be broken in to smaller units.
• Alternately stated, discrete production is obtained for those inputs which are counted.
• Example: Ploughing, Weeding, Irrigation etc.

Short Run Production Function (SRPF)

• Production Function in which some inputs or resources are fixed.

Y = f (X1 / X2, X3, ………….., Xn)

• Eg: Law of Diminishing returns or Law of variable proportions

Long Run Production Function (LRPF)

• Production function which permits variation in all factors of production.

Y = f (X1, X2, X3, ……………., Xn)

• Eg: Returns to scale
• The production function can be expressed in three ways:

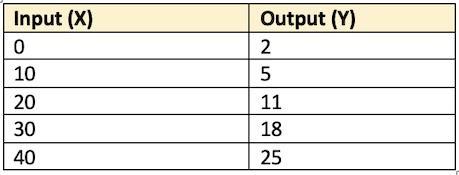
1. Tabular Form

• Production function can be expressed in the form of a table, where one column represents input, while another indicates the corresponding total output of the product.
• The two columns constitute production function.

  

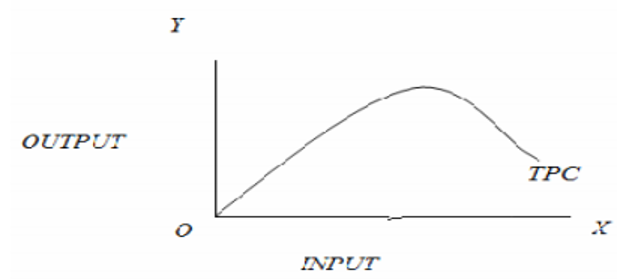
2. Graphical Form

• The production function can also be illustrated in the form of a graph, where horizontal axis (X axis) represents input and the vertical axis (Y axis) represents the output.

  

3. Algebraic Form

• Algebraically production function can be expressed as:

Y= f(X)

• Where,
  • Y represents dependent variable, output (yield of crop, livestock enterprise) and
  • X represents independent variable, input (seeds, fertilizers, manure etc),
  • f = denotes function of
• When a greater number of inputs is involved in the production of a product, the equation is represented as

Y = f(X1, X2, X3, X4 ……… Xn)

• In case of single variable production function, only one variable is allowed to vary, keeping others constant, can be expressed as

Y = f(X1 | X2, X3 ………. Xn)

• The vertical bar is used for separating the variable input from the fixed input. The equation denotes that the output Y depends upon the variable input X1, with all other inputs held constant.
• If more than one variable input is varied and few others are held constant, the relationship can be expressed as

Y = f(X1, X2 | X3, X4 …….. Xn)

Linear production function

Y = a + bX (Linear production function)

• Where
  • Y is dependent variable,
  • a is constant,
  • b is coefficient,
  • X is independent variable
• The constant ‘a’ represents the amount of product obtained from the fixed factor if none of the variable input is applied, while b is the amount of output produced for each unit of X (input) applied.

Cobb Douglas Production Function:

• Cobb Douglas propounded that output is a function of labour and capital. UPPSC 2021

Q = K L ^α C ^β

• Where, Q = Production; L = Labour and C = Capital.
• In the production function, solved by Cobb-Douglas, the share of labour was 3/4 and that of capital 1/4.

Y = K L ^3/4 C^1/4

• Here α + β = 1, it means Law of Constant Return to scale.
• After changing the value of power of labour and capital i.e. α and β, the different laws of production function can be explained
• When,
  • α + β = 1 means Law of Constant Return to Scale
  • α + β > 1 means Law of Increasing Return to Scale.
  • α + β < 1 means Law of Diminishing Return to Scale.
• When α + β = 1, it is a Linear Homogeneous Production Function at constant return if function is taken in Logarithm (Log) but not in natural scale.
• Cobb-Douglas function has constant Elasticity of substitution.

Types of Production Functions

• Linear Production Function: When production function is homogeneous of the first degree.

y = a₀ + a₁X₁ + a₂X₂ +……….+ a_nX_n

• where, y = production, a₀ = constant
• a₁, a₂ ……………. a_n = coefficient factors
• X₁, X₂, ……………..X_n = factors of production
• Quadratic production Function

y = a + bx + cx²

• where, a, b, c = constant,
• x = Production factor
• Square Root Production Function:

y = a + b √X₁+ cX₂

• Cubic Production Function:

y = a₀ + a₁ X + a₂X₂ + a₃X₃

• It is the systematic way of showing the relationship between different amounts of inputs that can be used to produce a product and the corresponding output of that product.
• Definition: Production function is a technical and mathematical relationship describing the manner and the extent to which a particular product depends upon the quantities of inputs or input services, used at a given level of technology and in a given period of time. In short, the relationship between input and output is termed as production function.

Types of Production Functions

Continuous Production Function:

• This is obtained for those inputs which can be split up in to smaller units.
• All those inputs which are measurable give raise to continuous production function.
• Example: Fertilizers, Seeds, Plant protection …

Become Successful With AgriDots

Learn the essential skills for getting a seat in the Exam with tons of fun in the process.

🦄 You are a pro member!

Only use this page if purchasing a gift or enterprise account

Yo! You just found a 20% discount using 👉 EASTEREGG

High-quality fitted cotton shirt produced by Next Level Apparel