Summary of basic production relationships

Returns to Scale

• By returns to scale, it is meant the behaviour of production when all factors (inputs) are increased or decreased simultaneously in the same proportion.
• Scale relationship refers to simultaneous change in all the resources in the same proportion. In other words, in returns to scale, we analyze the effect of doubling, trebling and so on of all inputs on the output.
• In returns to scale, all the necessary factors of production are increased or decreased to the same extent so that whatever the scale of production, the proportion among the inputs remain the same.
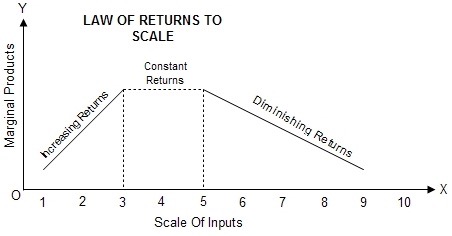
• When all inputs are increased, in unchanged proportions, the scale of production is expanded, the effect on output shows three stages:
  • Firstly, returns to scale increase because the increase in total output is more than proportional to increase in all inputs.
  • Secondly, returns to scale become constant as the increase in total product is an exact proportion to the increase in inputs.
  • Lastly, returns to scale diminish because the increase in output is less than proportionate to increase in inputs.

Example

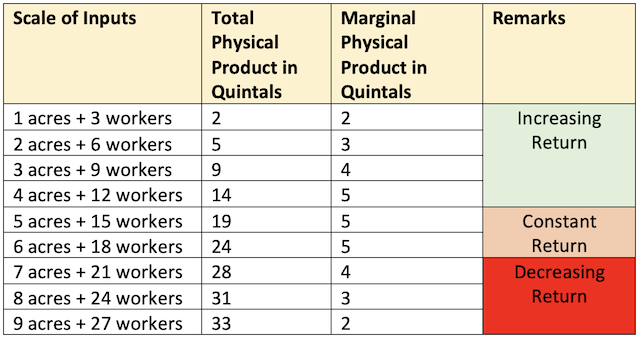
• In the above example, we see that when we employ one worker on three acres of land, the total product is 2 quintals. Now to increase the output, we double the scale, but the total product increases to more than double (5 quintals instead of 4 quintals). When the scale is trebled, the total product increases from 5 quintals to 9 quintals - the increase this time being 4 quintals as against 3 quintals. In other words, returns to scale have been increasing. If the scale of production is further increased, the Marginal Physical Product remains constant up to certain point and beyond it starts diminishing.
• Returns to scale are more theoretical interest than being relevant to actual practice. In practice, it is the law of variable proportions which has universal applications.
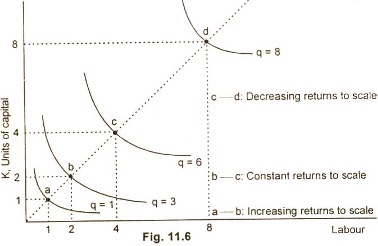
• Returns to scale can also be explained by using the knowledge of scale line and that of isoquant map. In the case of constant returns to scale, the distance between successive isoquants is constant i.e., AB = BC = CD.
• The distance goes on widening between the successive isoquants and diminishing returns operate i.e., AB < BC < CD.
• Finally, in the case of increasing returns to scale, the distance between the successive isoquants becomes smaller and smaller as we move away from the origin on the isoquant map i.e., AB> BC> CD.

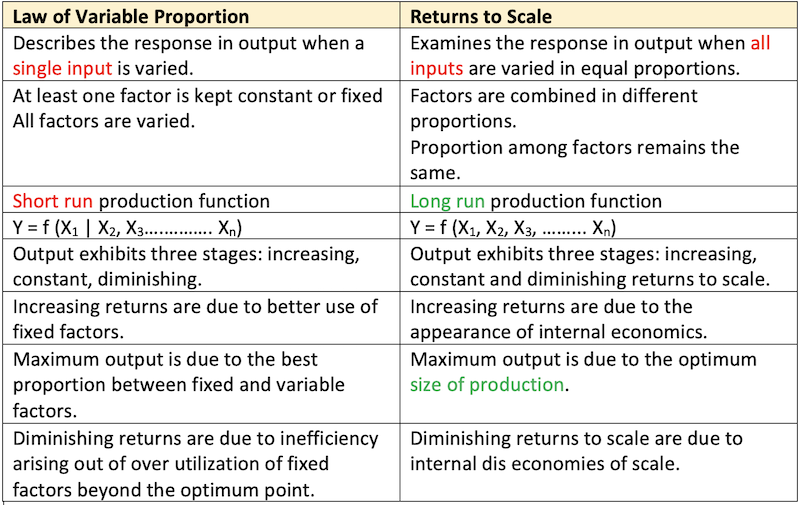
Differences between Law of variable Proportion and Returns to scale

Summary of basic production relationships

Returns to Scale

• By returns to scale, it is meant the behaviour of production when all factors (inputs) are increased or decreased simultaneously in the same proportion.
• Scale relationship refers to simultaneous change in all the resources in the same proportion. In other words, in returns to scale, we analyze the effect of doubling, trebling and so on of all inputs on the output.
• In returns to scale, all the necessary factors of production are increased or decreased to the same extent so that whatever the scale of production, the proportion among the inputs remain the same.
• When all inputs are increased, in unchanged proportions, the scale of production is expanded, the effect on output shows three stages:
  • Firstly, returns to scale increase …

Yo! You just found a 20% discount using 👉 EASTEREGG

High-quality fitted cotton shirt produced by Next Level Apparel